🎾 青学网球部的终极训练——不二周助的线段树之谜⚡️

🌟 题目描述

青学网球部最近迎来了一位神秘的训练顾问——三船入道教练！他提出了一套名为「究极线段树」的特训方案，准备彻底提升青学所有队员的实力。大家刚刚从紧张的地区大赛中恢复过来，还在为接下来的全国大赛做好准备，这时候，三船教练的到来无疑给了他们新的动力。

🏅 三船入道的“究极线段树”训练

在一个阳光明媚的下午，三船入道站在青学网球场的中央，指着排成一排的网球🎾说道：“今天，我们将迎来一场前所未有的训练！”他缓缓抬起手，示意队员们集合，“这一次，训练不仅仅是体力的比拼，还有你们的脑力挑战！”

不二周助站在队伍的最前面，平静地扫视着每一颗网球。队员们也都知道，今天的训练必定不同寻常，因为三船教练从不做无意义的训练。突然，三船入道开口了：“这次的训练，我要求你们在最短的时间内完成几个任务。你们每个人都有一个网球，网球上的训练值会随着不同的操作发生变化。你们的任务是利用高效的算法来计算训练值。”

队员们纷纷点头，而越前龙马🐱‍👤看似不经意地向不二周助投来一个眼神，显然他知道，不二周助将会是这次训练的关键人物。

“第一项任务——乘法强化特训！”三船入道猛地一拍手，“越前，带领大家进行扣杀训练。训练过程中，每个网球的训练值将被乘以一个指定的数。”越前龙马带着队员们迅速投入训练，网球的训练值在不知不觉中发生了变化。

🍀 加分激励特训

紧接着，河村隆💪开始了他的一轮加油训练。队员们站在场地上，随着河村的大喊和加油声，网球的训练值也随之增加。“每个人都加油，要让自己成为更强的选手！”河村隆的呐喊震撼全场。训练值继续被增加，队员们感到力量和气势的提升。

然而，三船教练并没有停止，他的目光锐利：“我知道你们很努力，但接下来的任务才是最具挑战性的。”他说完，手指向远处的网球堆。

🎯 训练值总和考核

三船入道看向不二周助，眼中带着些许期待：“不二，你来解决最后的难题吧。”

不二周助深吸一口气，走到场中央，他轻轻拿起一颗网球，低声自语：“这次，我们要利用线段树的算法来计算网球的训练值总和，并且做取模运算，必须尽快完成。”他转身对队员们说道：“你们将分别进行区间乘法、区间加法以及区间查询总和操作，我会通过线段树来快速处理这些任务。”

越前龙马疑惑地问：“不二，能不能简短解释一下，我们怎么用线段树来做这些操作？”

“不需要太多复杂的操作，”不二周助平静地答道，“我们会用线段树来帮助你们处理区间操作。通过这颗树，可以高效地计算出区间内的训练值总和，而对于乘法和加法操作，树会自动帮你们调整。”

队员们点点头，显然，他们已经进入了“究极线段树”特训的状态。

🏆 目标——全国大赛！

随着训练的深入，队员们逐渐掌握了线段树的使用技巧，不仅能够高效计算区间和，还能应对快速的区间乘法与加法操作。每次特训后，不二周助都会及时报告训练值的总和，并对模数进行取模。

这次训练不仅考验了大家的网球技术，更是一次智力上的挑战。通过不二周助的引导，队员们不仅学会了高效处理复杂的区间操作，也更加强了彼此之间的配合和默契。

“我们的目标只有一个——全国大赛！”不二周助最后说道，眼中闪烁着坚定的光芒，“这次特训将让我们变得更强！”

📥 输入格式

第一行包含三个整数 $n,q,m$，分别表示网球🎾的个数、特训操作的总数、以及训练值取模的模数；

第二行包含 $n$ 个整数，其中第 $i$ 个整数代表第 $i$ 个网球的初始训练值；

接下来 $q$ 行，每行描述一个特训操作，具体为：

• 操作 $1$：1 x y k 含义：区间 $[x,y]$ 内每个网球的训练值乘以 $k$；

• 操作 $2$：2 x y k 含义：区间 $[x,y]$ 内每个网球的训练值加上 $k$；

• 操作 $3$：3 x y 含义：查询区间 $[x,y]$ 内每个网球的训练值之和对 $m$ 取模后的结果。

📤 输出格式

对于每次“训练值总和考核”（操作3），输出一行，表示该次特训考核的结果。

🌟 输入输出样例

📌 输入示例

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

🎖️ 输出示例

17
2

🎾 样例解释（配合下图）

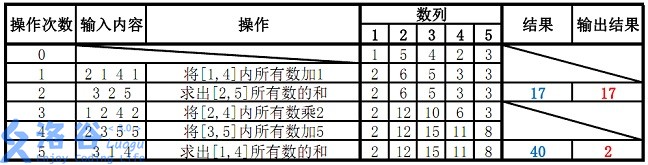
• 一开始5个网球训练值为 [1,5,4,2,3]；
• 🍀 第一次操作后训练值为 [2,6,5,3,3]；
• 🎯 第二次考核操作（2~5）为 $6+5+3+3=17$；
• 🔥 第三次操作后训练值为 [2,12,10,6,3]；
• 🍀 第四次操作后训练值为 [2,12,15,11,8]；
• 🎯 第五次考核操作（1~4）为 $2+12+15+11=40$，模38后为2。

🚩 数据范围与提示

• 对于 $30%$ 的数据：$n \le 8$，$q \le 10$；
• 对于 $70%$ 的数据：$n \le 10^3$，$q \le 10^4$；
• 对于全部数据：$1 \le n \le 10^5$，$1 \le q \le 10^5$，$1\le k\le 10^4$；
• 除样例外，数据统一为 $m = 571373$。

✨ 不二周助，快来帮助青学全队完成「究极线段树」特训吧！ 🍀🎾🚀